RESEARCH ARTICLE
Global Stability and Optimal Control Analysis of Malaria Dynamics in the Presence of Human Travelers
Samson Olaniyi1, Kazeem O. Okosun2, *, Samuel O. Adesanya3, 5, Emmanuel A. Areo4
Article Information
Identifiers and Pagination:
Year: 2018Volume: 10
First Page: 166
Last Page: 186
Publisher ID: TOIDJ-10-166
DOI: 10.2174/1874279301810010166
Article History:
Received Date: 6/8/2018Revision Received Date: 27/9/2018
Acceptance Date: 16/10/2018
Electronic publication date: 30/11/2018
Collection year: 2018

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Introduction:
The impact of unguarded human movement on the spread of infectious disease like malaria cannot be underestimated. Therefore, this study examines the significance of short term human travelers on malaria transmission dynamics.
Methods:
A non-autonomous system of ordinary differential equations incorporating four control strategies, namely personal protection, chemo-prophylaxis, chemotherapy and mosquito-reduction effort is presented to describe the dynamics of malaria transmission between two interacting populations. Suitable Lyapunov functions are constructed to analyze the global dynamics of the autonomous version. Moreover, the model which incorporates time-dependent vigilant controls is qualitatively analyzed with the overall goal of minimizing the spread of malaria and the associated costs of control implementation using the optimal control theory. An iterative method of forward-backward Runge-Kutta fourth order scheme is used to simulate the optimality system in order to investigate the effects of the control strategies on the magnitude of infected individuals in the population.
Results:
Analysis of the autonomous system shows that the disease-free equilibrium is globally asymptotically stable whenever the basic reproduction is less than unity and a uniquely determined endemic equilibrium is shown to be globally asymptotically stable whenever the associated basic reproduction number exceeds unity. In the case of non-autonomous system, necessary conditions for the optimal control of malaria are derived. It is shown that adherence to the combination of the control strategies by short term human travelers helps in curtailing the spread of malaria in the population.
1. INTRODUCTION
Malaria is a vector-borne disease caused by parasites of genus Plasmodium whose life cycle depends on the asexual and sexual phases in humans and mosquitoes respectively [1]. The disease is transmitted to humans through the bites of infected female Anopheles mosquitoes. Of the five parasites species that affect humans, Plasmodium falciparum and Plasmodium vivax pose the greatest public health challenge [2]. It is estimated that 212 million cases of malaria occurred globally in the year 2015 with most cases and deaths in the WHO African, South-East Asia and Eastern Mediterranean Regions [3].
The spread of malaria disease in two interacting populations of humans and mosquitoes has been described mathematically via compartmental models governed by autonomous and non-autonomous systems of ordinary differential equations. These models have helped in facilitating the understanding of mechanisms involved in the transmission dynamics of malaria [4-11] and some of the references therein. A comprehensive survey of malaria models starting from the basic Ross model [12] has been provided in Mandal et al., [13]. Particularly, the advent of the non-autonomous systems of ordinary differential equations in the description of malaria dynamics can be of great importance in assessing the impact of some intervention strategies, namely vector control, chemoprevention and case management on the disease transmission. Using optimal control theory, a number of studies of non-autonomous malaria models have been carried out. Blayneh et al., [14] presented an optimal control framework to examine the effects of time-dependent prevention and treatment efforts on malaria. Makinde and Okosun [15] analyzed the dynamics of malaria infection with infected immigrants by incorporating treatment of infectives and spray of insecticides as control functions.
In another development, Agusto et al., [16] applied optimal control theory to investigate optimal strategies for controlling the spread of malaria using treatment, insecticide treated bed nets and spray of mosquito insecticide as the system control variables, while Ozair et al., [17] analyzed the dynamics of vector-borne disease with nonlinear incidence using similar control variables. Lashari et al., [18] explored the impact of three control variables, namely vector-reduction, personal protection and blood screening strategies, on malaria dynamics with direct and indirect transmissions. Moreover, optimal vaccination and bed-net control efforts in populations with different levels of naturally acquired immunity were presented by Prosper et al., [19]. In Otiento et al., [20], the transmission dynamics of malaria was studied by considering four time-dependent control measures which include insecticide treated bed nets (ITNS), treatment, indoor residual spray (IRS), and intermittent preventive treatment of malaria in pregnancy (IPTp).
This paper presents an optimal control framework that does not only consider treatment control measure aimed at the blood-stage infection of malaria in infectious human but also considers a prophylactic measure targeted at treating liver-stage infection in latently infected (exposed) human among other intervention measures, namely mosquito-reduction and personal protection efforts. A class of short term vigilant human travelers who adhere to these control measures are incorporated into the human population. Using stability theory of nonlinear ordinary differential equations, global dynamics of the autonomous version of the formulated model is rigorously analyzed. Optimal control analysis is carried out on the time-dependent model using Pontryagin’s Maximum Principle in order to determine necessary conditions for the optimal strategies for controlling the spread of malaria.
The rest of this work is organized as follows. In Section 2, the model with four time-dependent control functions is presented and the qualitative analysis of its time-independent version is carried out. Further, in Section 2, optimal control analysis of the time-dependent model using Pontryagin’s Maximum Principle and numerical simulations are performed. Section 3 discuses results by showing the significance of different combinations of the control measures on the malaria dynamics. The work is wrapped up by giving some concluding remarks.
2. MATERIALS AND METHODS
2.1. Model Formulation
The model presented in this section takes into account time-dependent control functions such as personal protection, treatments (liver and blood stage therapies) and mosquito reduction intervention strategies. The total human population at time t, denoted by Nh (t), is subdivided into susceptible Sh (t) (number of individuals not yet infected with malaria parasite but are capable of being infected by infectious mosquitoes at time t; exposed Eh(t) (number of individuals infected with parasite still at the liver stage but not yet infectious at time t; infectious Ih(t) (number of individuals with malaria parasite at the blood stage and are capable of transmitting the disease to susceptible mosquitoes at time t; and vigilant Vh (t) (comprises number of human travelers who are protected against malaria for the entire duration of their short stay in the community). Then,
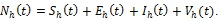 |
(1) |
The total mosquito population at time t, denoted by Nh (t), is subdivided into susceptible Sm(t) (number of mosquitoes not yet infected with malaria parasite but are capable of being infected by infectious humans at time t); exposed Em (t) (those infected but not yet infectious at time t); infectious Im (t) (those that are capable of transmitting malaria parasite to the susceptible humans at time t), so that
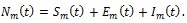 |
(2) |
It is assumed that new recruits enter human population by birth or immigration at the rate Λh. A fraction (1 - τ) Λh enters susceptible population while the remaining fraction τΛh are short term travelers who enter the community taking antimalarial measures daily for the entire duration of their short stay and then leave without getting infected. This class of of short term travelers are assumed to be protected against malaria infection. The disease transmission terms for humans and mosquitoes populations given, respectively, by
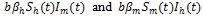 are reduced by a factor of (1 - u1 (t)), where b is the biting rate of mosquitoes, βh (βm)represents the transmission probability in humans (mosquitoes) and
are reduced by a factor of (1 - u1 (t)), where b is the biting rate of mosquitoes, βh (βm)represents the transmission probability in humans (mosquitoes) and 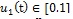 represents control variable for personal protection using ITNs and mosquito repellent lotion.
represents control variable for personal protection using ITNs and mosquito repellent lotion.
Exposed human progresses at per capita rate αh either to become infectious or recovered due to chemo-prohylaxis (liver-stage therapy) and travel out of the community without re-infection. Thus, control variable u2 (t) represents the use of liver-stage therapy which measures the level of effective treatment effort. It is worth stating that P. vivax malaria has ability to form dormant liver stages (hypnozoites) which often escape blood-stage therapy (WHO [2] and Howes et al., [21]). Hence, the need for the control variable u2 (t). Infectious human joins the class of vigilant human travelers at per capita recovery rate u3 (t)γ, where γ > 0 is a rate constant and 0 ≤ u3 (t) ≤ 1 represents control on treatment of infectious human targeted at blood stage parasites. It is assumed that recovery of infected humans is not spontaneous but depends only on treatment (liver and blood stage therapies). Every treated individual who recovers is allowed to enter vigilant class and individuals in this class are protected against infection.
The descriptions of variables and parameters used for the model are given in Table 1.
| Variable/Parameter | Description |
|---|---|
| Sh (t) | Number of susceptible humans |
| Eh (t) | Number of exposed or latently infected humans |
| Ih (t) | Number of infectious humans |
| Vh (t) | Number of vigilant short-term human travelers |
| Sm (t) | Number of susceptible mosquitoes |
| Em (t) | Number of exposed mosquitoes |
| Im (t) | Number of infectious mosquitoes |
| u1 (t) | Personal protection using insecticide-treated bed nets (ITNs) or mosquito-repellent lotion |
| u2 (t) | Chemo-prophylactic measure or liver-stage therapy for latently infected humans |
| u3 (t) | Chemotherapy or treatment of infectious humans |
| u4 (t) | Mosquito-reduction effort using indoor residual spray (IRS) |
| Λh | Recruitment rate of humans |
| τ | Fraction of recruitment rate of humans who are short-term travelers |
| Λm | Recruitment rate of mosquitoes |
| b | Mosquito biting rate |
| βh | Transmission probability per contact of susceptible humans with infectious mosquitoes |
| βm | Transmission probability per contact of susceptible mosquitoes with infectious humans |
| µh | Natural per capita death rate of humans |
| µm | Natural per capita death rate of mosquitoes |
| αh | Per capita progression rate of exposed humans |
| αm | Per capita progression rate of exposed mosquitoes |
| γ | Recovery rate constant of control |
| r | Rate constant of control |
The recruitment rate of the mosquito population assumed susceptible, denoted by Λm, is reduced by a factor (1 - u4 (t)) and each class of the mosquitoes population is reduced at a rate u4 (t)r, where r > 0 is a rate constant and u4 (t) is the control function due to spray of insecticides. Exposed mosquito becomes infectious at per capita rate αm. The death rates of humans and mosquitoes populations are given by µh and µm respectively.
The transmission dynamics of the disease is described by the following non-autonomous system of differential equations:
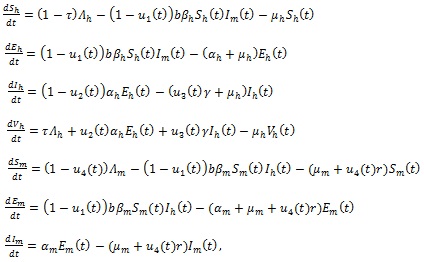 |
(3) |
with initial data given at t = 0.
2.2. Global Dynamics of the Autonomous Version
In the absence of the four time-dependent control functions (i.e., when u1 (t) = 0, u2 (t) = 0, u3 (t) = 0 and u4 (t) = 0), the non-autonomous model (3) becomes the following autonomous system of ordinary differential equations:
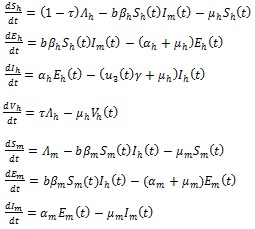 |
(4) |
The dynamics of system (4) is studied in the feasible region of the form:
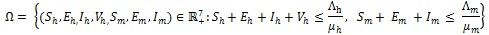 |
which can be shown to be positively invariant with respect to (4).
2.2.1. Global Stability of the Disease-Free Equilibrium (DFE)
The DFE of the model (4) is given by
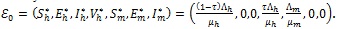 |
(5) |
Using the next generation matrix method [22], the basic reproduction number of model (4) is given by
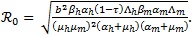 |
(6) |
Other methods for calculating 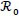 are provided in van den Driessche [23]. Straightforward calculation shows that
are provided in van den Driessche [23]. Straightforward calculation shows that
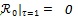 . This implies that if all individuals recruited into human population are vigilant, then there will not be malaria infection in the population. However, it is assumed that
. This implies that if all individuals recruited into human population are vigilant, then there will not be malaria infection in the population. However, it is assumed that
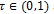 and all other parameters are positive. The dynamical behavior of autonomous system (4) as its solutions approach the disease-free is provided in Theorem 1.
and all other parameters are positive. The dynamical behavior of autonomous system (4) as its solutions approach the disease-free is provided in Theorem 1.
Theorem 1: If, 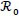 ≤ 1 then the DFE ε0 given by (5) is globally asymptotically stable in the region Ω.
≤ 1 then the DFE ε0 given by (5) is globally asymptotically stable in the region Ω.
Proof: Consider the constructed Lyapunov function of the form
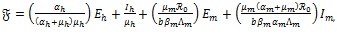 |
(7) |
with the time derivative of along
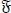 the solutions of system (4) given by
the solutions of system (4) given by
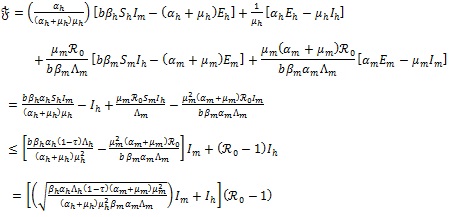 |
(8) |
Therefore,
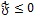 provided
provided
 if and only if
if and only if 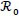 = 1 or Ih = 0 and Im = 0. It follows that the largest invariant set in {S, Eh, Ih, Vh, Sm, Em, Im)
= 1 or Ih = 0 and Im = 0. It follows that the largest invariant set in {S, Eh, Ih, Vh, Sm, Em, Im)
 } is the singleton {ε0 }, and hence by LaSalle’s invariance principle [24], the DFE {ε0 } is globally asymptotically stable. This completes the proof.
} is the singleton {ε0 }, and hence by LaSalle’s invariance principle [24], the DFE {ε0 } is globally asymptotically stable. This completes the proof.
The epidemiological implication of Theorem 1 is that malaria elimination is possible regardless of the initial sizes of the sub-populations of the model (4) whenever 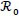 ≤ 1. This result is graphically illustrated in Fig. (7).
≤ 1. This result is graphically illustrated in Fig. (7).
2.2.2. Global Stability of the Endemic Equilibrium
First, the existence of endemic equilibrium (where the components of the infected variables are non-zero) of the model (4) is explored. Let the endemic equilibrium be represented by
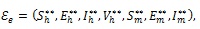 |
(9) |
and solving (4) at steady-state gives
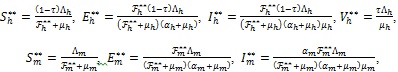 |
(10) |
with forces of infection for humans and mosquitoes at steady-states given, respectively, by
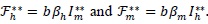 |
(11) |
Substituting (10) and the expression for
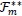 in (11) into the expression for
in (11) into the expression for
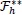 in (11) gives the following linear equation:
in (11) gives the following linear equation:
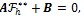 |
(12) |
where
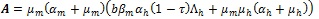 which is always positive since
which is always positive since
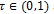 and
and
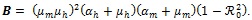 . It is should be noted from (12) that
. It is should be noted from (12) that
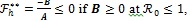 and no endemic equilibrium exits. On the other hand
and no endemic equilibrium exits. On the other hand
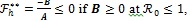 . Thus, an endemic equilibrium exists only at
. Thus, an endemic equilibrium exists only at 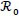 > 1 and this result is summarized hereunder.
> 1 and this result is summarized hereunder.
Theorem 2: The autonomous model (4) has a unique endemic (positive) equilibrium whenever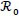 > 1, and no endemic equilibrium otherwise.
> 1, and no endemic equilibrium otherwise.
Next, the global stability property of the endemic equilibrium εe of the model (4) is explored in Theorem 3 with graphical illustration given in Fig. (7).
Theorem 3:If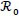 > 1, then the endemic equilibrium εe, of the autonomous model (4), given by (9) is globally asymptotically stable in the interior of the region Ω.
> 1, then the endemic equilibrium εe, of the autonomous model (4), given by (9) is globally asymptotically stable in the interior of the region Ω.
Proof: The use is made of the following Goh-Volterra type Lyapunov function [25-28].
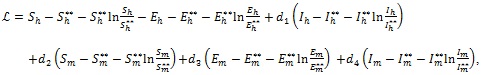 |
(13) |
with suitably determined coefficients,
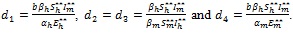 The time derivative of
The time derivative of  in (13) along the solutions of the model (4) is given by
in (13) along the solutions of the model (4) is given by
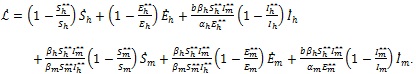 |
(14) |
The following equilibrium relations hold from (4) at steady-state:
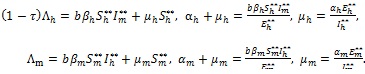 |
(15) |
Substituting appropriate equations of model (4) and the equilibrium relations (15) into (14) with algebraic simplification gives
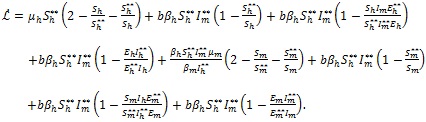 |
(16) |
Consequently,
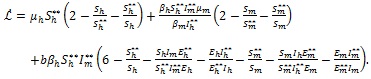 |
(17) |
Finally, since arithmetic mean is greater than or equal to geometric mean, it follows that
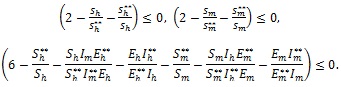 |
Therefore,
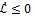 since all the model parameters are positive, with
since all the model parameters are positive, with
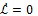 if and only if
if and only if
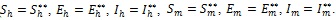 It follows from this that Vh →
It follows from this that Vh →
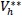 as t → ∞, and hence by LaSalle’s invariance principle [24], the endemic equilibrium Ee is globally asymptotically stable whenever
as t → ∞, and hence by LaSalle’s invariance principle [24], the endemic equilibrium Ee is globally asymptotically stable whenever 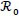 > 1. The proof is complete.
> 1. The proof is complete.
The epidemiological implication of the Theorem 3 is that malaria will establish itself in the community whenever 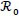 > 1 irrespective of the initial sizes of the infectious individuals in the population.
> 1 irrespective of the initial sizes of the infectious individuals in the population.
2.3. Optimal Control Analysis
In this section, the detailed qualitative analysis of the non-autonomous model (3) is carried out using Pontryagin’s Maximum Principle. The bulk of models in the literature of mathematical epidemiology that uses optimal control theory depends on the Pontryagin’s Maximum Principle [29-31]. This is so because necessary conditions for the optimal strategies aimed at controlling the disease spread can explicitly be derived using Pontryagin’s Maximum Principle [32]. For a collection of these models, readers may check Sharomi and Malik [33]. The following objective functional 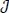 is used to minimize the number of exposed human Eh (t), infectious human Ih (t) and total mosquito population Nm (t) while keeping the costs of applying the controls u1 (t), u2 (t), u3 (t) and u4 (t) as low as possible.
is used to minimize the number of exposed human Eh (t), infectious human Ih (t) and total mosquito population Nm (t) while keeping the costs of applying the controls u1 (t), u2 (t), u3 (t) and u4 (t) as low as possible.
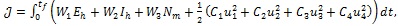 |
(18) |
where W1, W2, W3, C1, C2, C3 and C4 are positive weight constants. The terms
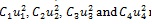 represent the costs associated with personal protection efforts, liver-stage therapy, treatment of infectious human and spraying of insecticides respectively. The costs of controls have been chosen to be quadratic in accordance with the standard in the literature [33].
represent the costs associated with personal protection efforts, liver-stage therapy, treatment of infectious human and spraying of insecticides respectively. The costs of controls have been chosen to be quadratic in accordance with the standard in the literature [33].
Thus, the goal is to seek an optimal control quadruple 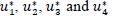 such that
such that
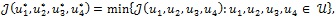 |
(19) |
where
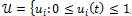 Lebesgue measurable
Lebesgue measurable
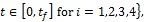 is the control set. The Pontryagin’s Maximum Principle [32] converts system (3), with (18) and (19) into a problem of minimizing pointwise a Hamiltonian H, with respect to u1, u2, u3 and u4.
is the control set. The Pontryagin’s Maximum Principle [32] converts system (3), with (18) and (19) into a problem of minimizing pointwise a Hamiltonian H, with respect to u1, u2, u3 and u4.
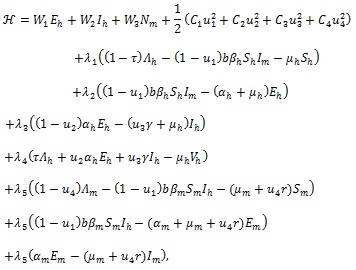 |
(20) |
where λi, = 1, 2,...,7 are the adjoint variables. Using the existence result for the optimal control [34], the following theorem is obtained.
Theorem 4: There exists an optimal control quadruple 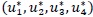 that minimizes
that minimizes 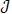 over
over 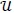 subject to the state system (3). Further, there exist adjoint variables λi, = 1, 2,...,7 satisfying
subject to the state system (3). Further, there exist adjoint variables λi, = 1, 2,...,7 satisfying
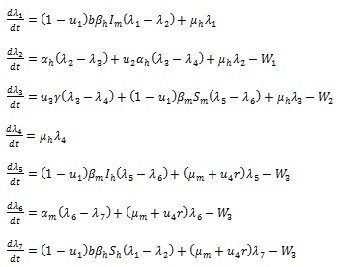 |
(21) |
with transversality conditions
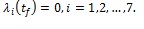 |
(22) |
Further, the optimal controls 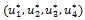 are given by
are given by
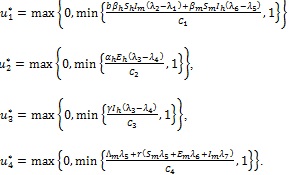 |
(23) |
Proof: The existence of optimal control follows from Fleming and Rischel [34] due to convexity of the integrand of the objective functional 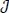 in (18) with respect to ui i = 1,....,4, over a convex and closed control set
in (18) with respect to ui i = 1,....,4, over a convex and closed control set 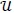 , and system (3) satisfies the Lipschitz property with respect to the state variables since the state solutions are bounded. The differential equations (21) governing the adjoint variables λi i = 1, 2,....,7, are obtained by partial differentiation of the Hamiltonian
, and system (3) satisfies the Lipschitz property with respect to the state variables since the state solutions are bounded. The differential equations (21) governing the adjoint variables λi i = 1, 2,....,7, are obtained by partial differentiation of the Hamiltonian 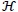 in (20) with respect to the corresponding state variables, so that
in (20) with respect to the corresponding state variables, so that
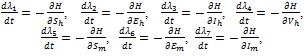 |
with terminal conditions (22). The characterization of the optimal control given by (23) is derived by taking the partial derivative of Hamiltonian (20) with respect to each of the control ui, and solving
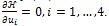 . This ends the proof.
. This ends the proof.
2.4. Numerical Simulations
The optimality system of fourteen-dimensional ordinary differential equations consisting the state and the adjoint equations (3) and (21) respectively is solved using an iterative method with Runge-Kutta fourth order scheme. The state equations are solved forward in time with an initial guess for the controls over the simulated time. Owing to the transversality conditions (22), the adjoint equations are solved backward in time using the current iteration solutions of the state equations. Then the controls are updated by using a convex combination of the previous controls and the value from the characterization (23). This process continues until the difference between the values of unknowns at the previous iteration and that of the present iteration is negligibly small [35].
The parameter values provided in Table 2 are used so that 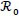 = 3.94178 > 1. The simulations of the model are done by using the initial conditions given by Sh (0) = 100, Eh (0) = 25, Ih (0) = 15, Vh (0) = 5, Sm (0) = 1000, Em (0) = 20 and Im (0) = 30. For the purpose of illustrating the optimal level of treatment control combined with other efforts required to minimize number of infected humans and total mosquito population as well as minimizing the associated costs of controls, the weight constants values in the objective functional (18) are chosen so that W1 = 1, W2 = 1.5, C1 = 0.02, C2 = 0.2, C3 = 0.15, and C4 = 0.5
= 3.94178 > 1. The simulations of the model are done by using the initial conditions given by Sh (0) = 100, Eh (0) = 25, Ih (0) = 15, Vh (0) = 5, Sm (0) = 1000, Em (0) = 20 and Im (0) = 30. For the purpose of illustrating the optimal level of treatment control combined with other efforts required to minimize number of infected humans and total mosquito population as well as minimizing the associated costs of controls, the weight constants values in the objective functional (18) are chosen so that W1 = 1, W2 = 1.5, C1 = 0.02, C2 = 0.2, C3 = 0.15, and C4 = 0.5
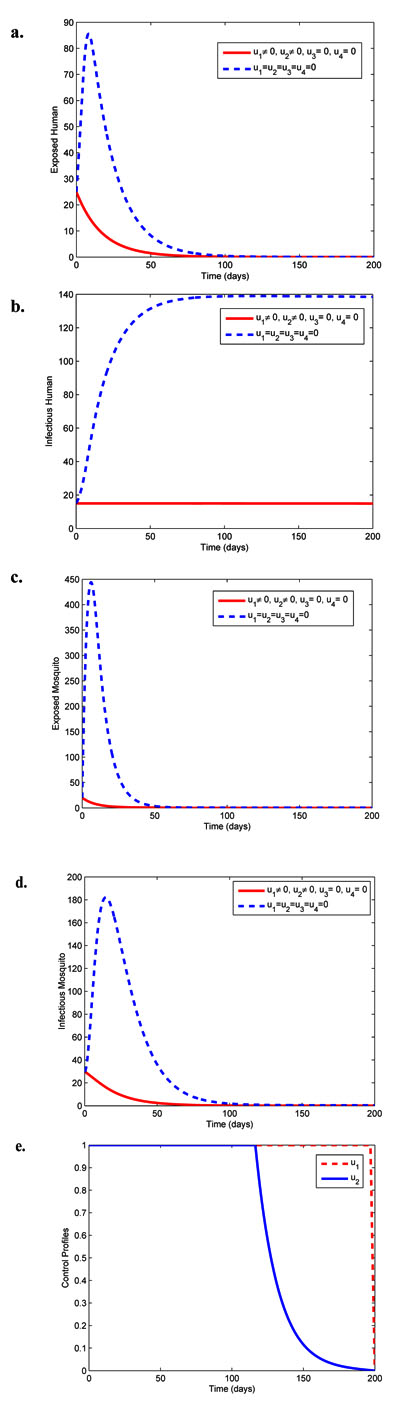 |
Fig. (1). Simulations showing effects of personal protection (u1) and chemo-prophylaxis (u2) on malaria spread. |
| Parameter | Value | Source |
|---|---|---|
| Λh | 0.000215 | [36] |
| Λm | 0.071 | [25] |
| µh | 0.0000548 | [36] |
| µm | 0.066 | [14] |
| αh | 1/17 | [14] |
| αm | 1/18 | [14] |
| b | 0.12 | [36] |
| βh | 0.03 | [8], [16] |
| βm | 0.09 | [14], [15] |
| γ | 0.05 | Assumed |
| r | 0.04 | [14] |
| τ | 0.25 | Assumed |
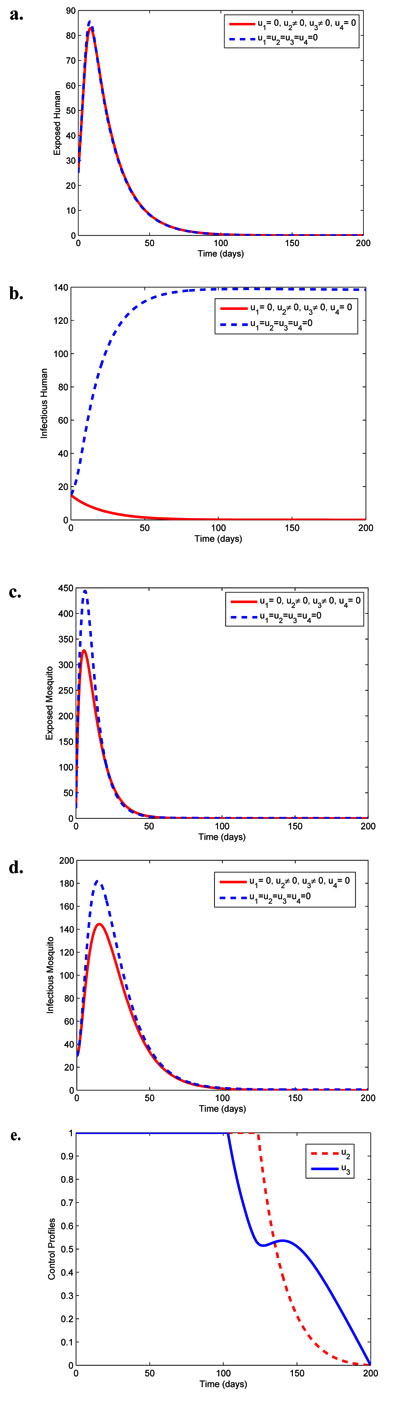 |
Fig. (2). Simulations of model (3) showing effects of chemo-prophylaxis (u2) and treatment (u3) on malaria spread. |
3. RESULTS AND DISCUSSION
Fig. (1) illustrates the combined effects of the preventive control u1 and liver-stage treatment control u2 on malaria transmission within human and mosquito populations. It is observed that the sizes of exposed human, exposed and infectious mosquitoes with control diminish more rapidly than the case without control. The size of infectious human in Fig. (1b) with control is constantly maintained at the initial condition. The control profiles in Fig. (1e) shows that the optimal control u1 is at the upper bound for 198 days before dropping to the lower bound while the control u2 is at the upper bound until time t = 120 days before reducing gradually to the lower bound at the final time.
As it can be seen in Fig. (2), combination of the treatment controls u2 and u3 causes a sharp decrease in the number of infectious human. The reduction in the sizes of other classes is not as sharp as when compared with scenario in Fig. (1). The optimal controls u2 and u3 shown in Fig. (2a) are at the upper bound till about 125 days and 105 days respectively before dropping gradually until reaching the lower bound in the final time.
Fig. (3) illustrates the combined effect of preventive and therapeutic controls on the dynamical spread of malaria. It can be observed that the numbers of exposed and infectious human and mosquito diminish more rapidly with controls than when there is no control. Fig. (3e) reveals that preventive control u1 should be sustained maximally for 165 days before reducing to zero in final time. The optimal controls u2 and u3 in Fig. (3e) are at the upper bound for about 98 and 105 days respectively before decreasing to the lower bound in final time.
 |
Fig. (3). Simulations of model (3) showing effects of personal protection (u1), chemo-prophylaxis (u2) and treatment (u3) on malaria spread. |
Fig. (4) shows the impact of the three controls u2, u3 and u4 in reducing malaria in the population. As shown in Fig. (4e), the treatment controls u2 and u3 should be sustained maximally until 120 and 110 days respectively while u4 is at the upper bound for 198 days before dropping to zero in final time.
 |
Fig. (4). Simulations of model (3) showing effects of chemo-prophylaxis (u2), treatment (u3) and indoor residual spray (u4) on malaria spread. |
In Fig. (5), the control profiles illustrating the combination of other optimal controls without blood-stage control u3 are displayed. The behavior of the sizes of human and mosquito populations is similar to that in Fig. (1). However, it can be seen in Fig. (5a) that the control u2 is at the upper bound for about 138 days and the control u4 is at the upper bound for 198 days before dropping to the lower bound at the final time.
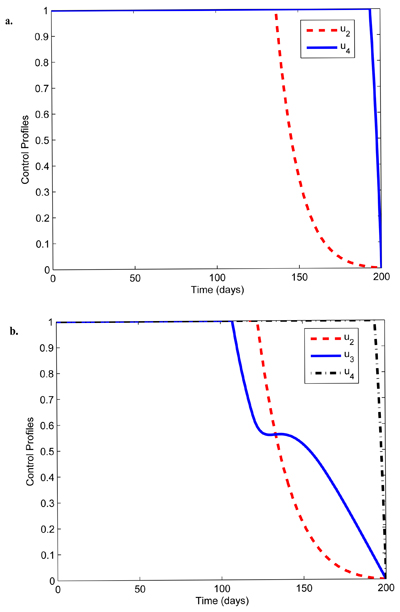 |
Fig. (5). Control profiles showing combination of personal protection (u1), chemo-prophylaxis (u2), and indoor residual spray (u4). |
Further, in Fig. (5b), the control u1 is at the upper bound for 119 days and the control u2 is at the upper bound for about 117 days while the control u4 should be sustained maximally until about 198 days before reducing to the lower bound.
Fig. (6d) reveals that control u1 is at the upper bound for 100 days, control u2 is at the upper bound for 90 days and control u3 is at the upper bound for 100 days while control u4 should be sustained maximally for about 198 days before dropping to the lower bound at the final time. Fig. (7a) depicts the global asymptotic behaviour of the infectious human at the disease-free equilibrium (5) using the parameter values in Table 2 except that µh = 0.05, βm = 0.01, τ = 0.95 such that  = 2.73496 x 10-4 < 1 where the disease dies out regardless of large initial values of the infectious human population. On the other hand, Fig. (7b) shows the global asymptotic behaviour of the infectious human at the endemic equilibrium (9) using the same parameter values in Table 2 for which
= 2.73496 x 10-4 < 1 where the disease dies out regardless of large initial values of the infectious human population. On the other hand, Fig. (7b) shows the global asymptotic behaviour of the infectious human at the endemic equilibrium (9) using the same parameter values in Table 2 for which  > 1 where the disease persists regardless of the initial sizes of the infectious human population.
> 1 where the disease persists regardless of the initial sizes of the infectious human population.
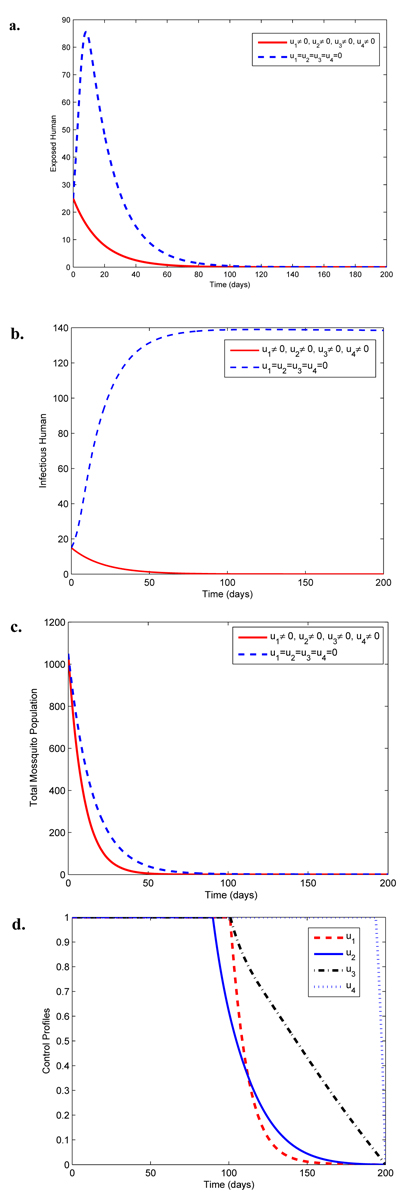 |
Fig. (6). Simulations of model (3) illustrating effects of all the four controls on malaria spread. |
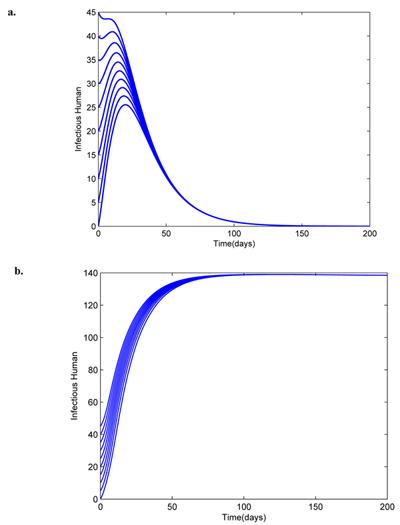 |
Fig. (7). Global asymptotic dynamics of the disease-free and endemic equilibrium points. |
CONCLUSION
The malaria transmission dynamics in the presence of human travelers who are protected against malaria has been analyzed both theoretically and quantitatively. The work is distributed in two parts; autonomous and non-autonomous systems of ordinary differential equations.
The global asymptotic properties of the autonomous version with respect to the disease-free and endemic equilibria are established. The disease-free equilibrium is shown to be globally asymptotically stable when 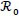 < 1 and a uniquely determined endemic equilibrium of the autonomous system is shown to be globally asymptotically stable when
< 1 and a uniquely determined endemic equilibrium of the autonomous system is shown to be globally asymptotically stable when 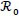 > 1. This shows that the global dynamics of the autonomous model is completely determined by the epidemiological threshold
> 1. This shows that the global dynamics of the autonomous model is completely determined by the epidemiological threshold 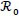 which measures the spread potential of malaria in the community.
which measures the spread potential of malaria in the community.
In other words, our results ascertain that effective control or elimination in the community depends largely on the basic reproduction number and therefore, efforts that seek the reduction of this basic reproduction number should be encouraged in order to achieve a malaria-free population.
On the other hand, optimal control analysis is performed on the non-autonomous system which incorporates four time-dependent controls, namely liver and blood stage therapies as well as mosquito-reduction strategy using insecticide spray and personal protection effort using insecticide treated bed nets. The analysis made possible by Pontryagin’s Maximum Principle coupled with numerical simulations reveal that the combination of the four control strategies may be adopted in curtailing the spread of malaria among the human and mosquito interacting populations.
Hence, individuals traveling into a malaria-endemic region for a short period of time are enjoined to be vigilant by taking into account the combination of the aforementioned control measures with a view to preventing further spread of the disease beyond the malaria endemic region.
It is worth mentioning that the present model is formulated under the assumption that treated individuals travel out of the community without getting re-infected due to strict adherence to control measures. However, further studies may consider re-infection of treated individuals as a result of imperfect treatment or human’s failure to adhere strictly to the control measures.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No Animals/Humans were used for studies that are base of this research.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
KOO wishes to acknowledge and appreciate the support of National Research Foundation, South African, through Grants numbers 115029 and 115524. The authors are grateful to the anonymous referees and the handling editor for their helpful comments that led to an improved manuscript.









